|
Носителями тока в металлах являются свободные электроны, т.е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком Паулем Друде (1863 – 1906) и разработанной впоследствии нидерландским физиком Г.Лоренцем , а также на ряде классических опытов, рассмотренных в предыдущем параграфе.
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики Ньютона. Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.
Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По теории Друде – Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории, можно найти среднюю скорость теплового движения электронов
которая для Т = 300 К равна 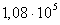 м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока. м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
При наложении внешнего электрического поля на металлический проводник кроме силового движения электронов возникает их упорядоченное движение, т.е. возникает электрический ток. Среднюю скорость 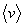 упорядоченного движения электронов можно оценить согласно формуле для плотности тока: упорядоченного движения электронов можно оценить согласно формуле для плотности тока:
Выбрав допустимую плотность тока, например для медных проводов получим, что при концентрации носителей тока средняя скорость упорядоченного движения электронов равна . Следовательно, << т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях модуль результирующей скорости можно заменить модулем скорости теплового движения .
Вывод основных законов электрического тока в классической теории электропроводности металлов:
1. Закон Ома. Пусть в металлическом проводнике существует электрическое поле напряженностью Е = const. Со стороны поля заряд е испытывает действие силы F = eE и приобретают ускорение
Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
где  – среднее время между двумя последовательными соударениями электрона с ионами решетки. – среднее время между двумя последовательными соударениями электрона с ионами решетки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдаст им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
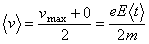 |
(23.1) |
|

![]() столкновений:
столкновений:![]() столкновений и решетке передается энергия
столкновений и решетке передается энергия

![]() является удельной тепловой мощностью тока. Коэффициент пропорциональности между
является удельной тепловой мощностью тока. Коэффициент пропорциональности между ![]() и
и ![]() по (23.2) есть удельная проводимость
по (23.2) есть удельная проводимость ![]() ; следовательно, выражение закон Джоуля – Ленца в дифференциальной форме:
; следовательно, выражение закон Джоуля – Ленца в дифференциальной форме:

